Las figuras geométricas forman parte fundamental de las matemáticas y de nuestro entorno cotidiano.
Desde los objetos que nos rodean hasta las construcciones más complejas, todo está compuesto por formas como cuadrados, rectángulos, triángulos y círculos.
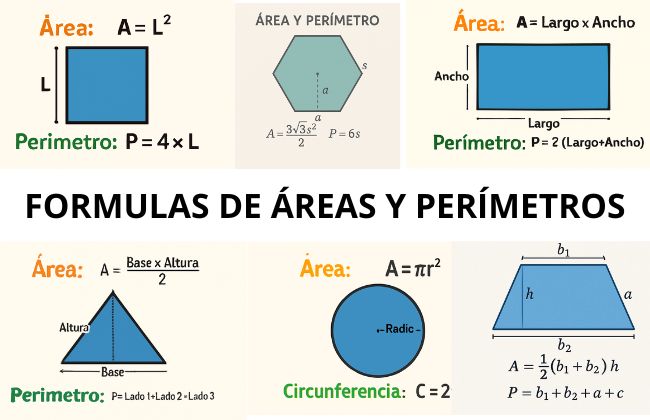
Comprender el área y el perímetro de estas figuras es esencial, ya que nos permite calcular el espacio que ocupan y la longitud de sus bordes.
Es un conocimiento útil tanto en la vida diaria como en campos profesionales como la arquitectura, el diseño y la ingeniería.
El área nos indica la cantidad de superficie que cubre una figura plana, mientras que el perímetro nos dice cuánto miden sus bordes al sumarlos.
Saber cómo calcular estas medidas nos ayuda a resolver problemas prácticos, como saber cuánta pintura se necesita para una pared o cuánta cerca se requiere para rodear un terreno.
En este post exploraremos cómo calcular áreas y perímetros de diversas figuras geométricas, acompañados de ejercicios y ejemplos claros fáciles de entender.
Índice de contenidos
¿Qué son el área y el perímetro?
Definición de área
El área mide el espacio bidimensional que ocupa una figura. Piensa en el área como la cantidad de pintura necesaria para cubrir una superficie completamente plana.
Se mide en unidades cuadradas, como metros cuadrados (m²), centímetros cuadrados (cm²) o kilómetros cuadrados (km²).
Por ejemplo:
- Un rectángulo de 4 metros de largo y 3 metros de ancho tendrá un área de:
Área del rectángulo = 4{largo} x 3{ancho} = 4 m x 3 m = 12 m².
Definición de perímetro
El perímetro, por otro lado, es la medida de la longitud total de los bordes de una figura. En otras palabras, es la «cinta» necesaria para rodear el contorno.
Su unidad es lineal, como metros (m), centímetros (cm) o millas (mi).
Por ejemplo:
- Si tienes un cuadrado con lados de 5 metros, el perímetro será:
Perímetro del cuadrado= 5m(lado 1) + 5m(lado 2) + 5m(lado 3) + 5m(lado 4) = 20 m.
Unidades de medida para áreas y perímetros
Para Perímetros
Longitud, por lo tanto, se mide en unidades lineales:
- Milímetros (mm)
- Centímetros (cm)
- Metros (m)
- Kilómetros (km)
Para Áreas
Se mide en unidades cuadradas:
- Milímetros cuadrados (mm²)
- Centímetros cuadrados (cm²)
- Metros cuadrados (m²)
- Kilómetros cuadrados (km²)
Es fundamental recordar que las unidades de área son siempre el cuadrado de las unidades de longitud.
Fórmulas de figuras geométricas de área y perímetro
1. Área y perímetro de un cuadrado
Imagina que tienes un cuadrado, y uno de sus lados mide L (como una regla que mide lo mismo en todos sus lados).
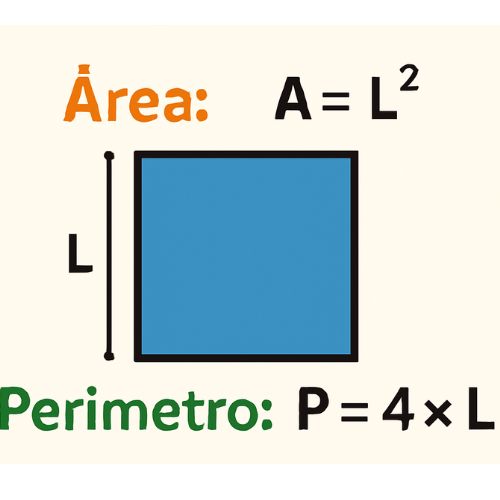
Área: Para encontrar el área del cuadrado, simplemente multiplicas el tamaño de un lado por sí mismo.
La fórmula es: Área =L×L=L²
Esto significa que el área es el espacio que cubre el cuadrado. Si cada lado mide 3, el área será 3 × 3 = 9.
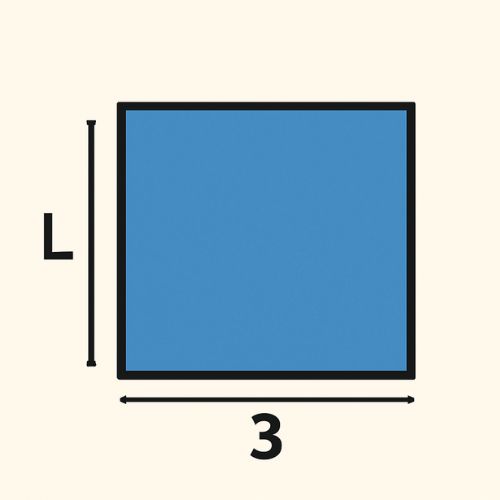
Perímetro: El perímetro es la distancia total alrededor del cuadrado. Como el cuadrado tiene 4 lados iguales, la fórmula es:
Perímetro del cuadrado =4×L
Si cada lado mide 3, entonces el perímetro será 4 × 3 = 12.
2. Área y perímetro de un rectángulo
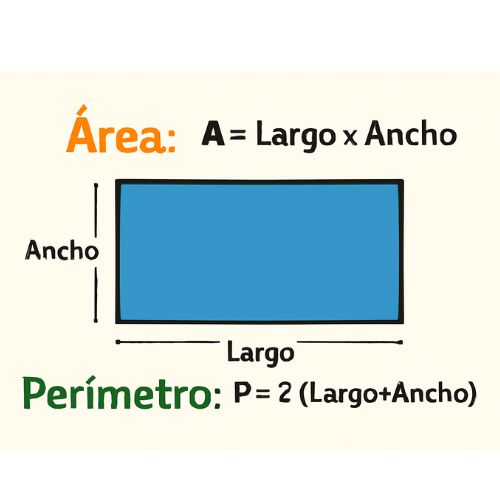
Área del rectángulo:
El área es el espacio dentro del rectángulo. Para encontrarla, multiplicamos el largo por el ancho.
Así: Área = Largo × Ancho
Ejemplo:
Si un rectángulo tiene un largo de 4 y un ancho de 3, entonces:
Área=4×3=12. Así que, en este caso, el área del rectángulo sería 12 unidades cuadradas.
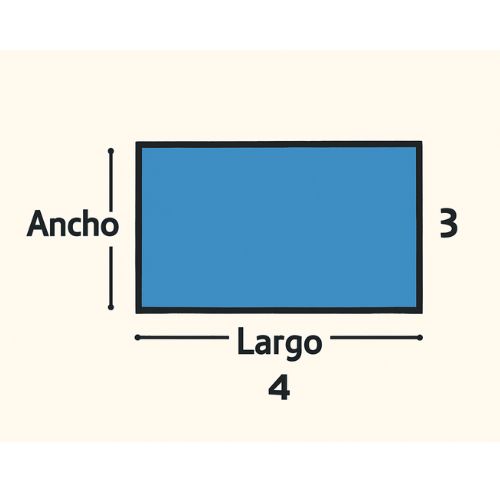
Perímetro del rectángulo:
El perímetro es la distancia alrededor del rectángulo, es decir, la suma de los cuatro lados. Como el rectángulo tiene dos lados largos y dos lados cortos, la fórmula es:
Formula del Perímetro del rectángulo =2× (Largo +Ancho)
Ejemplo:
Si el largo es 4 y el ancho es 3, entonces:
Perímetro=2×(4+3)=2×7=14. Así que, en este caso, el perímetro del rectángulo sería 14 unidades.
Resumen:
- Área: Se multiplica el largo por el ancho.
- Perímetro: Se suma el largo y el ancho, y luego se multiplica por 2.
3. Área y perímetro de un triángulo
Área del triángulo:
El área de un triángulo es el espacio dentro del triángulo. Para encontrar el área, necesitamos saber la base (la parte más ancha del triángulo) y la altura (la distancia desde la base hasta el vértice superior).
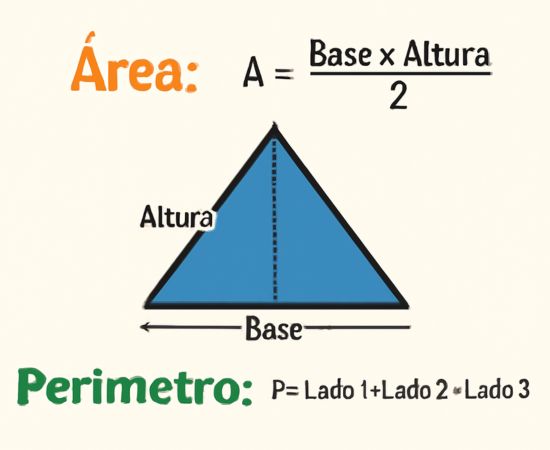
La fórmula para calcular el área del triángulo es:
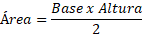
Ejemplo:
Si un triángulo tiene una base de 6 y una altura de 4, entonces:
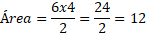
Entonces, el área del triángulo sería 12 unidades cuadradas.
Perímetro del triángulo:
El perímetro es la distancia alrededor del triángulo. Para encontrarlo, sumamos las longitudes de los tres lados del triángulo. Si conocemos las longitudes de los tres lados, simplemente sumamos:
Formula del Perímetro del triangulo = Lado 1+Lado 2+Lado 3
Ejemplo:
Si los tres lados del triángulo son 6, 5 y 7, entonces:
Perímetro=6+5+7=18
Entonces, el perímetro del triángulo sería 18 unidades.
Dato clave:
- Área del triángulo: Multiplicas la base por la altura y luego divides entre 2.
- Perímetro del triángulo: Sumamos las longitudes de los tres lados.
4. Área y perímetro de un círculo
Área del círculo:
El área de un círculo es el espacio que ocupa en el plano. Para encontrar el área de un círculo, necesitamos saber su radio. El radio es la distancia desde el centro del círculo hasta el borde.
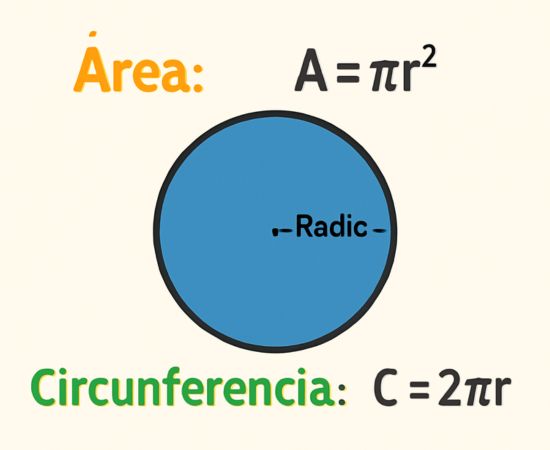
La fórmula para calcular el área de un circulo es:
Área=π×r²
Donde:
- π (pi) es un número especial que vale aproximadamente 3.14.
- r es el radio del círculo, o sea, la distancia desde el centro hasta el borde.
Ejemplo:
Si el radio del círculo es 3, entonces:
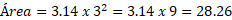
Entonces, el área del círculo sería 28.26 unidades cuadradas.
Perímetro o Circunferencia del círculo:
El perímetro de un círculo también se llama circunferencia, es la distancia alrededor del borde del círculo. Para encontrarla, usamos el radio nuevamente, pero en este caso la fórmula es:
Formula para calcular el perímetro de un circulo =2×π×r
Ejemplo:
Si el radio del círculo es 3, entonces:
Perímetro o Circunferencia=2×3.14×3=18.84
Entonces, la circunferencia del círculo sería 18.84 unidades.
Dato clave:
- Área: Multiplicas π por el radio al cuadrado.
- Circunferencia (Perímetro): Multiplicas 2×π por el radio.
5. Área y perímetro de un rombo
Área del rombo:
El área del rombo se calcula con la diagonal mayor (la línea más larga que conecta dos vértices opuestos) y la diagonal menor (la línea más corta que conecta los otros dos vértices opuestos).
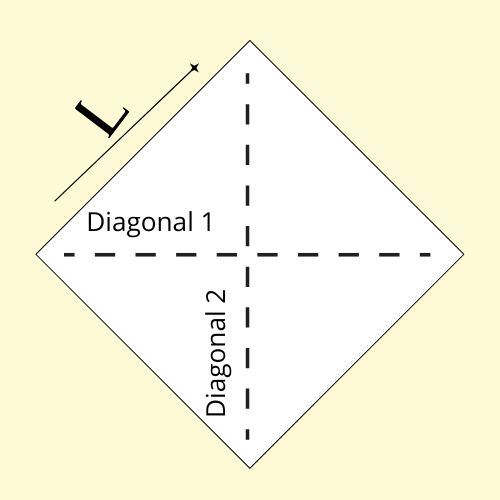
La fórmula para calcular el área de un rombo es:
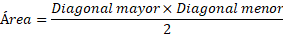
Ejemplo:
Si un rombo tiene una diagonal mayor de 8 y una diagonal menor de 6, entonces:
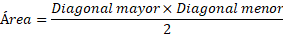
Entonces, el área del rombo sería 24 unidades cuadradas.
Perímetro del rombo:
El perímetro de un rombo es la suma de sus cuatro lados. Como todos los lados de un rombo son iguales, si conocemos el tamaño de uno de los lados, solo multiplicamos ese valor por 4.
La fórmula para el perímetro es:
Formula del Perímetro del rombo =4×L
Donde L es el largo de un lado del rombo.
Ejemplo:
Si un lado del rombo mide 5, entonces:
Perímetro=4×5=20. Entonces, el perímetro del rombo sería 20 unidades.
Dato clave:
- Área del rombo: Multiplicas la diagonal mayor por la diagonal menor y divides entre 2.
- Perímetro del rombo: Multiplicas el tamaño de un lado por 4.
6. Área y perímetro de un trapecio
Área del trapecio:
El área de un trapecio se calcula usando las bases (las dos líneas paralelas) y la altura (la distancia entre las dos bases).
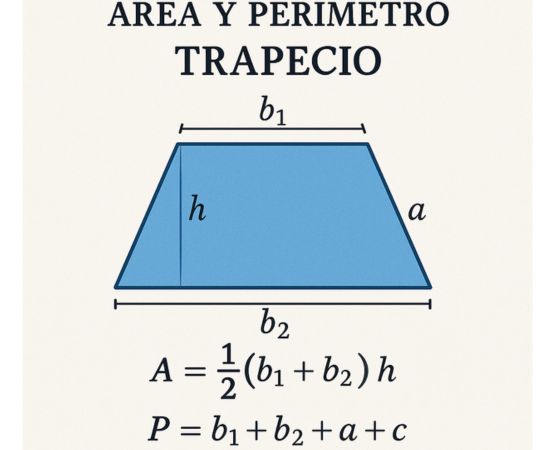
La fórmula para el área de un trapecio es:
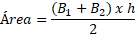
Donde:
- B1 es la base mayor.
- B2 es la base menor.
- h es la altura (la distancia entre las bases).
Ejemplo:
Si un trapecio tiene una base mayor de 8, una base menor de 5 y una altura de 4, entonces:
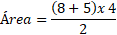
Entonces, el área del trapecio sería 26 unidades cuadradas.
Perímetro del trapecio:
El perímetro de un trapecio es la suma de los cuatro lados del trapecio. Necesitamos saber la base mayor, la base menor y las longitudes de los dos lados no paralelos (que se llaman lados oblicuos).
Fórmula del perímetro del trapecio= B1+B2+L1+L2
Donde:
- B1 es la base mayor.
- B2 es la base menor.
- L1 y L2 son los lados oblicuos.
Ejemplo:
Si el lado oblicuo 1 es 4, el lado oblicuo 2 es 4, la base mayor es 8 y la base menor es 5, entonces:
Perímetro = 8+5+4+4=21. Entonces, el perímetro del trapecio sería 21 unidades.
Dato clave:
- Área del trapecio: Se suman las bases, se multiplican por la altura y luego se dividen entre 2.
- Perímetro del trapecio: Se suman todas las longitudes de los lados.
Área y perímetro de un hexágono regular
Área del hexágono regular:
Un hexágono regular es un hexágono donde todos sus lados son iguales y todos sus ángulos son iguales.
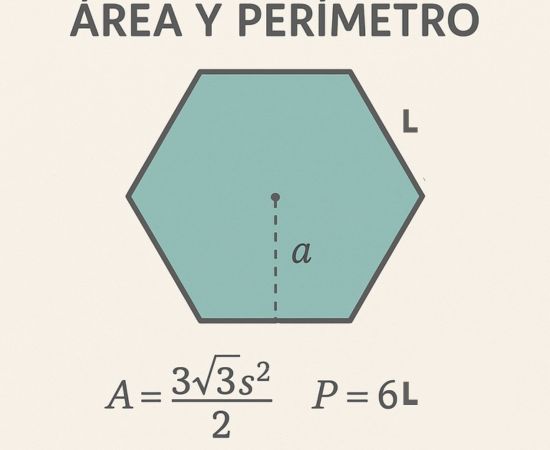
Para calcular el área de un hexágono regular, necesitamos conocer el largo de un lado (que llamaremos L) y usar una fórmula especial.
La fórmula para calcular el área de un hexágono regular es:
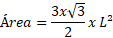
Donde:
- L es el largo de uno de los lados del hexágono.
- ∛ es la raíz cuadrada de 3, que vale aproximadamente 1.732.
Ejemplo:
Si el largo de un lado del hexágono es 4, entonces:
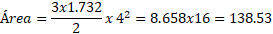
Entonces, el área del hexágono sería 138.53 unidades cuadradas.
Perímetro del hexágono:
El perímetro de un hexágono es la suma de las longitudes de sus 6 lados. Como todos los lados de un hexágono regular son iguales, basta con multiplicar el largo de un lado por 6.
Fórmula del perímetro para hexágono =6×L
Ejemplo:
Si el largo de un lado del hexágono es 4, entonces:
Perímetro=6×4=24. Entonces, el perímetro del hexágono sería 24 unidades.
Dato clave:
- Área del hexágono: Usamos una fórmula con el largo de un lado y una constante para obtener el área.
- Perímetro del hexágono: Multiplicamos el largo de un lado por 6.
Ejercicios de áreas y perímetros con respuestas
1. Pregunta: Si un cuadrado tiene un lado de 7 m, ¿cuál es su área y su perímetro?
Resolución:
Área: 𝐴 =7×7 = 49m²
Perímetro: 𝑃 = 4×7 = 28m
P=4×7=28m
Respuesta: Área = 49 m², Perímetro = 28 m.
2. Pregunta: Un rectángulo tiene un largo de 8 m y un ancho de 4 m. ¿Cuál es su área y su perímetro?
Resolución:
Área: 𝐴 = 8×4 = 32m²
A=8×4=32m²
Perímetro:
𝑃 =2×(8+4) = 2×12 = 24m
P=2×(8+4) = 2×12=24m
Respuesta: Área = 32 m², Perímetro = 24 m.
3. Pregunta: Un triángulo tiene una base de 10 cm y una altura de 6 cm. ¿Cuál es su área?
Resolución:
Área=
Respuesta: Área = 30 cm².
4. Pregunta: Un círculo tiene un radio de 3 cm. ¿Cuál es su área y su circunferencia?
Resolución:
Área: 𝐴 = 𝜋×3² = 3.14 × 9 = 28.26cm²
Circunferencia:
𝐶 = 2×𝜋×3 =2×3.14×3 = 18.84 cm
Respuesta: Área = 28.26 cm², Circunferencia = 18.84 cm.
5. Pregunta: Un trapecio tiene una base mayor de 10 cm, una base menor de 6 cm y una altura de 4 cm. ¿Cuál es su área?
Resolución:
Área:
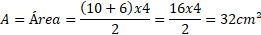
Respuesta: Área = 32 cm².
Vea También:
